Which Linear Inequality is Represented by the Graph?

A Detailed Guide

Understanding Which Linear Inequality is Represented by the Graph involves interpreting visual data on a coordinate plane. This process requires analyzing critical features of the graph, such as the boundary line and shaded region, to determine the correct inequality. This article will guide you through the steps to decode these graphical representations effectively.

Critical Components of a Linear Inequality Graph

To determine which linear inequality is represented by a graph, you need to understand its components:

• The Boundary Line

The boundary line is crucial in visualizing linear inequalities. This line divides the coordinate plane into two distinct regions. Here’s how to identify its significance:

• Solid Line: If the boundary line is solid, it indicates that the points on the line are included in the solution set. This means the inequality consists of “equal to” in its expression.
• Dashed Line: A dashed boundary line means the points on the line are not included in the solution set. Consequently, the inequality does not include “equal to” in its expression.

1. The Shaded Region

The shaded area of the graph represents all possible solutions to the inequality. Depending on whether the shading is above or below the boundary line, it signifies the direction of the inequality:

• Shaded Above the Line: If the shaded region is above the boundary line, the inequality symbol is typical “≥” or “>”.
• Shaded Below the Line: If the shaded area is below the line, the inequality symbol is generally “≤” or “<.”

Steps to Determine the Linear Inequality

To accurately determine the linear inequality from a graph, follow these steps:

• Find the Equation of the Boundary Line

The first step involves deriving the equation of the boundary line, which is typically in the slope-intercept form y=mx+by = mx + by=mx+b:

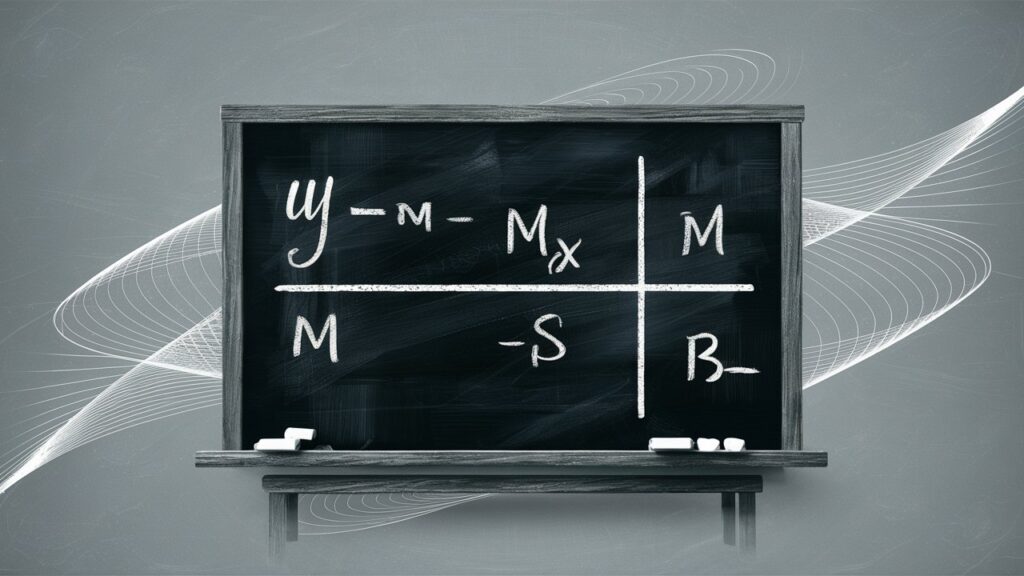
• Determine the Slope (m): Identify the Slope by calculating the rise over the run between two points on the boundary line. This Slope tells you how steep the line is.
• Find the Y-intercept (b): The y-intercept is where the line crosses the y-axis. This value represents the point where x=0x = 0x=0.

• Identify the Inequality Symbol

Based on the type of boundary line and shading, you can determine the correct inequality symbol:

• Solid Line: Use “≤” or “≥” if the line is solid.
• Dashed Line: Use “<” or “>” if the line is dashed.

To verify the inequality symbol:

• Select a Test Point: Choose a point in the shaded region of the graph (preferably one with easy coordinates like (0,0)).
• Substitute the Coordinates: Plug the coordinates of the test point into the equation of the boundary line.
• Check the Result: If the inequality holds, the symbol used in the graph is correct. If not, reverse the inequality symbol.

Example

Let’s go through an example to illustrate these steps:

Suppose you have a graph with the following features:

• A solid boundary line with a slope of 2.
• The y-intercept of -1.
• The shaded region is above the line.

To find the inequality:

• Equation of the Boundary Line: The equation is derived from the Slope and y-intercept:
• y=2x−1y = 2x – 1y=2x−1
• Determine the Inequality Symbol: Since the line is solid and the shaded region is above the line, the inequality is:
• y≥2x−1y \geq 2x – 1y≥2x−1

This equation represents all the points greater than or equal to 2x−12x – 12x−1, aligning with the graph’s shading.

Also Read: Artificial Intelligence: Unveiling the Power of Artificial Intelligence

Additional Tips

To improve your skills in determining linear inequalities from graphs:

• Practice Regularly: Work with various graphs to familiarize yourself with different boundary lines and shading types.
• Use Online Tools: Graphing calculators and online graphing tools can help verify your results and practice.
• Double-Check Work: Always recheck your process to ensure accuracy.

You can proficiently interpret linear inequalities from graphs by following these steps and regularly practicing. This skill is valuable in many areas of mathematics and real-world applications.